Evaporating a pot of water

As part of tutoring physics and maths to high school students, I sometimes write up deep-dive explanations of questions arising during lessons. The question below discusses how long it takes to completely evaporate a pot of water.

Steps involved in evaporating a pot of water.

---

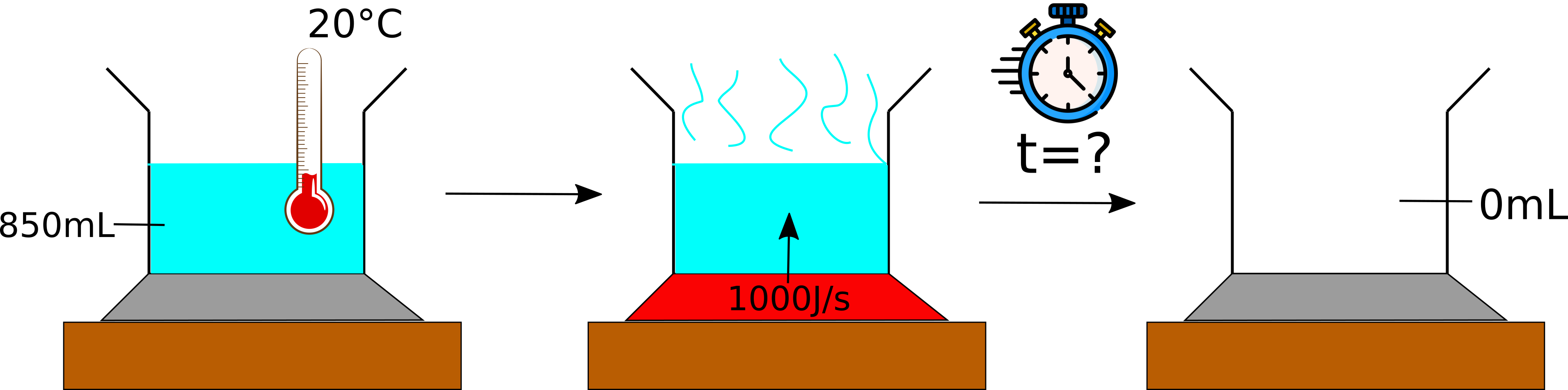
You have been given the question:

A pot containing 850 mL of water is sitting on a stove element. Initially, the water has a temperature of 20 °C. The element is turned on and delivers 1000 J per second. Calculate when the water is completely evaporated.

We’re now going to do a “deep dive” into the question, so buckle up!

Finding useful information in the question

Problem-solving tip: extract the essential information from the question to reduce the problem to its “bare bones”. Also, note any information about the problem’s context that might be relevant to solving the problem. This is something that takes practice and patience!

One strategy to solve a problem like the one we have is to read the entire question first before doing anything else to get a high-level overview of what’s being asked. Then we return to the beginning of the question and take each sentence one at a time and pull out the information that might be useful to us and categorise it somehow. For instance, in the first sentence

A pot containing 850 mL of water is sitting on a stove element.

the main piece of information is that we have 850 mL of water which will be heated up. The fact that it’s in a pot on a stove is only secondary; it could be in a glass flask on a heating element or could be in a plastic bowl in a microwave oven. What’s important here is that we have a certain amount of water and energy is going to be fed into it to heat it up.

Initially, the water has a temperature of 20 °C.

The water is at 20 °C before anything else happens to it. This is also a hint that the temperature is going to change somehow and that we’ve been given a reference temperature for later calculations.

The element is turned on and delivers 1000 J per second.

Fairly obviously, 1000 J of energy is being added to the water per second. This is the bit where we realise that it’s being heated up. However, this part of the question tells us exactly how: 1000 J for every second (which, incidentally, is 1000 W; a Watt is the amount of energy per unit time, in particular the number of Joules per second). We know from reading the whole question at the beginning that we have to calculate a time, so having time (i.e. seconds) turn up in one piece of information is very helpful to keep in the back of our heads for the remainder of the question.

Calculate when the water is completely evaporated.

The important words in this sentence are “when” and “evaporated”. We’ve thus been asked for an amount of time (“when”; which probably could be more precisely specified as “how many seconds are required to completely evaporate the water” or “how much time will pass before all the water has evaporated”). An amount of time links back to the energy rate we have from the previous sentence (1000 J/s is an energy rate: it is how much energy per unit time is being added to the system). The second important word “evaporated” tells us the final state of the system, i.e. all the liquid water has been turned into gaseous water (steam) and is thus “gone” into the air.

Using the words from the question, the task we’ve been asked to perform is thus reduced to:

850 mL water, 20 °C; 1000 J/s; when evaporated?

Another way to write the same thing¹ would be something like this, where we make time more explicit:

• t<=0: 850 mL water at 20 °C
• t=0: 1000 J/s
• t=? when water volume is 0 mL?

We could also look at this pictorially:

We have a rate of energy per unit time, thus if we know how much energy we need to completely evaporate the water, we can then work out how much time that will take (the energy rate is constant, which also makes things easier to calculate).

A physical intuition of the overall evaporation process

So how do we get from water at 20 °C to all of it being completely evaporated? This is a two-step process:

• heat the water to 100 °C
• convert the liquid water into gaseous water (steam).

Note that there’s a simplifying assumption being used here: evaporation doesn’t occur until the water has reached 100 °C. We know from experience that water doesn’t have to be boiling for it to evaporate, however in this case that process is much slower than how quickly the water is being heated by the stove element, thus we ignore any evaporation which might be happening as the water is heated from 20 °C to 100 °C.

That might sound a bit weird. After all, isn’t water at 100 °C boiling? And thus it’s already turning into steam? This is true to a degree, yet when water is boiling at 100 °C it is actually a mixture of liquid and gaseous water, both states being at 100 °C.²

When water is a gas, the water molecules have so much energy that they don’t interact with one another very much. The situation is very different in the liquid state: water molecules are held together by their intermolecular force, which is mostly due to hydrogen bonding but also partially due to the van der Waals force.

These bonds look something like this:

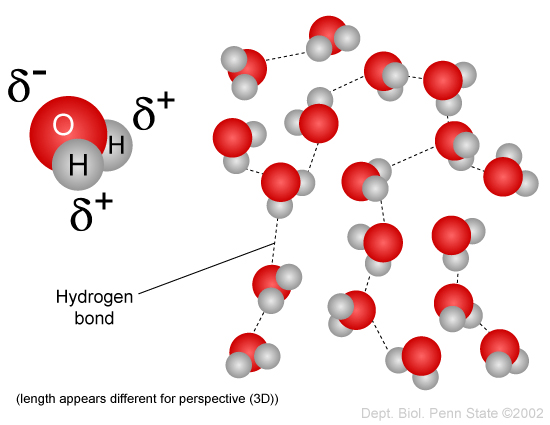
For liquid water to become a gas, these forces have to be overcome and that takes energy. Thus, we need two lots of energy to evaporate water: heat it to boiling point and then break the intermolecular bonds.

These two steps are governed by two pieces of thermodynamics: the specific heat capacity and the heat of vaporisation.³

The specific heat capacity is the amount of energy (per unit mass) that it takes to raise a substance by 1 °C. You will often see this written with units of \(\mathrm{\ J \cdot kg^{-1} \cdot K^{-1}}\), where a temperature change of 1 K is the same as a temperature change of 1 °C. Thus, the specific heat is what we can use to work out how much energy it will take to heat the water from 20 °C to 100 °C.

Note that replacing the temperature change units from K to °C works because the two temperature scales have the same slope, i.e. the markings on the scale of a thermometer using °C and one using Kelvin are the same distance apart. We can convince ourselves that temperature differences in both units have the same numerical value by converting each of the temperatures from °C to K. The formula is “Temperature in °C” + 273.15 K= “Temperature in K”. The interesting thing to note here is that there is no factor to be applied to the value of temperature in °C, or, written more explicitly, there is a factor of 1 K/°C (to get the right units). So we get

\[\begin{align} T_{\mathrm{diff}} &= (100 °C \cdot 1 K/°C + 273.15 K) - (20 °C \cdot 1 K/°C + 273.15 K)\\ &= 373.15 K - 293.15 K\\ &= 80 K \end{align}\]

in the same way that the difference 100 °C - 20 °C is 80 °C. This means that as long as we are dealing with temperature differences we can use either K or °C.

The heat of vaporisation is the amount of energy per unit mass required to change from the liquid into the gaseous state. This is sometimes quoted in units of J/g or kJ/kg, which is the same thing.

Unfortunately, the values for these parameters are not given in the question and hence we have to look them up and make some assumptions about which values we are expected to use (there is sometimes variation in which value one could use). This isn’t a problem because this is a much better reflection of how the real world works: if one doesn’t know what a certain parameter is, then one has to go looking for it and work out if the numbers one finds make sense in the given context. This is a really good situation because we’ve got a great opportunity to learn new things!

So what is the specific heat capacity for water? To find this out we can look up the value in a table of specific heat capacities and for water at 25 °C (close enough for our purposes) the value is 4.1813 \(\mathrm{\ J \cdot kg^{-1} \cdot K^{-1}}\).

And what about the heat of vaporisation? After a bit of looking around, we find a table on the Enthalpy of vaporisation Wikipedia page which lists values for common substances, one of which is water.

Note the comment on that same Wikipedia page:

The enthalpy of vaporization is often quoted for the normal boiling temperature of the substance.

The fact that the enthalpy of vaporisation is specified with respect to the normal boiling point backs up our intuition that the evaporation process is split into two parts: heating to the boiling point and then vaporising. Thus we can be more confident that we’re on the right path.

Building a physical intuition from experiment

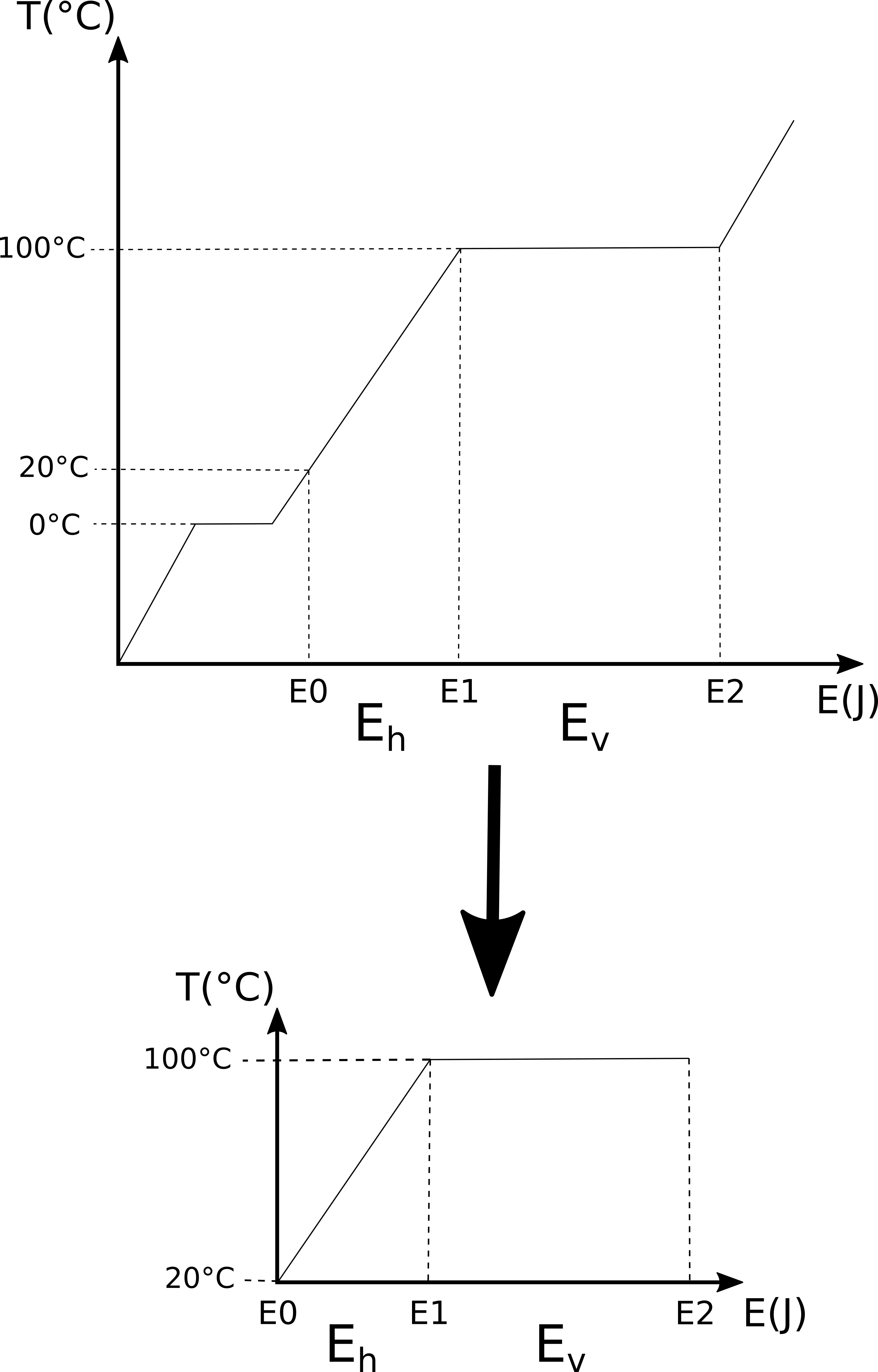
But you don’t have to take my word for it, you can make an experiment to try it out. The heating curves page of the University of Texas Chemistry 301 thermodynamics course describes this experiment. The setup they use is like the problem we’re trying to solve: take a beaker with ice in it and put it on a hot plate at a temperature well above 100 °C (in this case 120 °C). Through experience, we know that the ice will melt into water and as we add more heat to the water it will eventually boil. The temperature of the hot plate must be above the boiling point of water so that we know that the hot plate is always adding energy to the water. If we measure the temperature of the water as we add more energy, then we’ll see that the temperature will rise until we have an ice-water solution, at which point the temperature will stay constant at 0 °C until all the ice has melted. Once all the ice has melted, the water’s temperature will start rising again and at a rate proportional to the amount of energy we add to it per unit time. The temperature will keep rising until the water starts to boil and we have a water-steam mixture at a temperature of 100 °C. The water-steam mixture will stay at this temperature until all the water has evaporated into steam and then the temperature of the steam will continue rising in proportion to the amount of energy we’re adding per unit time. If we plot the temperature of the system against the energy we add to it, we get a heating curve like that shown below.

There’s an interesting point to make here: if we know we are adding energy to the system at a constant rate (as we are in the problem we’re trying to solve), then an x-axis of energy (Joules as in the graph above) is equivalent to an x-axis of time because time is directly related to energy through the energy rate (1000 J/s in the problem we want to solve). Thus the graph above could also be read as temperature changes over time.

This helps us better understand the problem we want to solve because we merely need to work out the point on the x-axis that matches 20 °C and then work out how much energy is required to get to the plateau at 100 °C. After that, we calculate the energy required to convert the water-steam mixture at 100 °C into all steam (i.e. all the water has evaporated).

Thus the problem we want to solve is a subset of the heating curve for water that we are now familiar with:

Calculating how long it takes for the water to evaporate

Let’s scale down the problem to consider heating only 1 mL of water from 20 °C to 100 °C (because 1 mL is easier to think about than 850 mL).

Heating the liquid water

The specific heat capacity of liquid water is 4184 J/kg/K and is sometimes quoted more approximately by 4.2 kJ/kg/K (where we use kJ to scale down the numerical value by a factor of 1000 (this makes the numbers easier to work with)) or equivalently 4.2 J/g/K (because the “kilo” part in kJ and kg cancel when dividing).

Thus, the energy to raise 1 g of water from 20 °C to 100 °C is (let’s call this the heating energy \(E_h = E_1 - E_0\); see also the heating curve diagram above):

\[\begin{equation} E_h(1\mathrm{\ g}) = 4.2 \mathrm{\ J/g/K} \cdot (100 - 20) \mathrm{\ K} = 336 \mathrm{\ J} \end{equation}\]

We can use Python in a Jupyter notebook to run the calculation. Enter the following code into a Jupyter notebook.

specific_heat_capacity = 4.2
boiling_temperature = 100
initial_temperature = 20

# energy to raise 1 g of water from 20 °C to boiling point
boiling_energy_1g = specific_heat_capacity * (boiling_temperature - initial_temperature)

print(f"Energy to raise 1 g of water from 20 °C to boiling point: {boiling_energy_1g} J")

Running the associated cell, you should get this output:

Energy to raise 1 g of water from 20 °C to boiling point: 336.0 J

However, we have a volume of water, not a weight, thus we need to work out how many grams there are in 1 mL of water. Water has a density of 0.9970474 g/mL at 25 °C, thus:

\[\begin{equation} 1\mathrm{\ mL\ of\ water} = 0.9970474\mathrm{\ g\ of\ water} \end{equation}\]

For our purposes, this is close enough to the value 1, so we can assume that 1 mL of water weighs 1 g. With this simplification in mind, we can say that the energy required to raise 1 mL of water from 20 °C to 100 °C (i.e. 80 °C) is:

\[\begin{equation} E_h(1\mathrm{\ mL}) = 4.2 \mathrm{\ J/g/K} \cdot (100 - 20) \mathrm{\ K} = 336 \mathrm{\ J} \end{equation}\]

Thus, to raise 850 mL of water by 80 °C (equivalently by 80K) is:

\[\begin{equation} E_h = 850 \mathrm{\ g} \cdot 4.2 \mathrm{\ J/g/K} \cdot (100 - 20) \mathrm{\ K} = 285600 \mathrm{\ J} \end{equation}\]

In a new cell in your Jupyter notebook, enter the following code:

specific_heat_capacity = 4.2
boiling_temperature = 100
initial_temperature = 20
water_volume = 850

# energy to raise given volume of water from 20 °C to boiling point
heating_energy = water_volume * specific_heat_capacity * (boiling_temperature - initial_temperature)
print(f"Energy to raise a volume of water from 20 °C to boiling point: {heating_energy} J")

Running this cell should give you this output:

Energy to raise a volume of water from 20 °C to boiling point: 285600.0 J

Turning boiling liquid water into steam

The heat of vaporisation for water is given as 2257 J/g or 2265 kJ/kg = 2265 J/g or 2260 kJ/kg depending upon where one looks. This is why it would have been helpful to have the expected values to use as part of the question. I don’t think the exact value matters that much really, so we’ll just use the value from the heat of vaporisation for water Wikipedia page, i.e. 2257 J/g.

We have 850 mL of water = 850 g of water at 100 °C. Thus the energy required to evaporate this amount of water is (let’s call this amount of energy \(E_v\); the energy of vaporisation):

\[\begin{equation} E_v = 2257 \mathrm{\ J/g} \cdot 850 \mathrm{\ g} = 1918450 \mathrm{\ J} \end{equation}\]

In another cell in your Jupyter notebook, enter the following code:

heat_of_vaporisation = 2257
water_volume = 850

# energy of vaporisation
vaporisation_energy = heat_of_vaporisation * water_volume
print(f"Energy of vaporisation: {vaporisation_energy} J")

Running this cell should give this result:

Energy of vaporisation: 1918450 J

An interesting point to note here is how large this value is in comparison to the energy required to boil the water: it’s almost 7 times as much energy! In other words, it takes much more energy to evaporate water as it does to simply heat it. Thus we can see that phase changes–such as transitioning from the liquid to the gaseous state–require a lot of energy.

Total energy and total time to evaporate water

The total energy we need to evaporate all the water, \(E_{\mathrm{tot}}\) is thus

\[\begin{equation} E_{\mathrm{tot}} = E_h + E_v = 285600 \mathrm{\ J} + 1918450 \mathrm{\ J} = 2204050 \mathrm{\ J} \end{equation}\]

Again, we can run this calculation ourselves by creating a new cell in the Jupyter notebook and entering this code:

total_energy = heating_energy + vaporisation_energy
print(f"Total energy required to evaporate water: {total_energy} J")

Running the cell gives:

Total energy required to evaporate water: 2204050.0 J

Since we know that we’re adding energy to the system at a rate of 1000 J/s, it will thus take \(E_{\mathrm{tot}}/1000\) s to evaporate all the water. I.e. the time to evaporate all the water, \(t_e\) is:

\[\begin{align} t_e &= 2204050 / 1000 \mathrm{\ s}\\ &= 2204.05 \mathrm{\ s}\\ &= 2204.05 / 60 \mathrm{\ minutes}\\ &= 36.73 \mathrm{\ minutes} \end{align}\]

To run the final calculation, enter the following code into a new cell in your Jupyter notebook:

evaporation_time_seconds = total_energy / 1000
print(f"Evaporation time (seconds): {evaporation_time_seconds}")
evaporation_time_minutes = evaporation_time_seconds / 60
print(f"Evaporation time (minutes): {evaporation_time_minutes:.2f}")

This should give you this output:

Evaporation time (seconds): 2204.05
Evaporation time (minutes): 36.73

In other words, it will take just over half an hour to evaporate all the water.  This result seems about right from previous experience one might have of boiling water on a stove. One could, of course, attempt this experiment at home (be careful!), to confirm the result of this calculation.

Returning to where we came from

Now that we’ve solved the problem and have found a solution, let’s summarise it to round off the discussion. We could describe the situation as follows:

To evaporate all the water, we need to first bring the water to boiling point and then vaporise the water. Given the heat capacity of water of 4.2 J/g/K, the temperature difference of 80K and the mass of water (850 mL = 850 g), it will take \(850\mathrm{\ g} \cdot 4.2 \mathrm{\ J/g/K} \cdot 80 \mathrm{\ K} = 285600\mathrm{\ J}\) to boil the water. Given the heat of vaporisation of \(2257 \mathrm{\ J/g}\) it will take \(850\mathrm{\ g} \cdot 2257 \mathrm{\ J/g} = 1918450\mathrm{\ J}\) to vaporise the water. The total energy required is thus \(285600 \mathrm{\ J} + 1918450 \mathrm{\ J} = 2204050\mathrm{\ J}\). At a constant rate of 1000 J/s, this will take \(2204050 \mathrm{\ J} / 1000 \mathrm{\ J/s} = 2204.05\mathrm{\ s}\) (approximately half an hour) to evaporate all the water.

And that’s it!

Trying out other ideas

As part of this exercise, you’ve created a Jupyter notebook with lots of information in it. You could try changing the initial temperature value (initial_temperature) to a different number and then re-run the entire notebook and see how long evaporation takes in that case. You can even start to think up crazy thought experiments like:

• how long would it take to evaporate a pot of water if the boiling point of water was 50 °C instead of 100 °C?
• how long would it take to evaporate a 10L bucket of water?
• how much energy does it take to evaporate an Olympic-sized swimming pool?
• how long would it take to evaporate a pot of ethanol?

Give it a go and see what happens!

1. Tip: rewording the same question in different ways gives a new perspective and sometimes brings insight into how to solve a given question. ↩

2. Note that the solid, liquid and gaseous states are also called “phases”, thus one can talk about when water is in the “gaseous phase” or equivalently the “gaseous state”. ↩

3. The heat of vaporisation is also called the enthalpy of vaporisation, the latent heat of vaporisation, or the heat of evaporation. ↩

Support

If you liked this post and want to see more like this, please buy me a coffee!