Sailplane glide distance
As part of tutoring physics and maths to high school students, I sometimes write up deep-dive explanations of questions arising during lessons. The question below discusses how far a glider will fly given a known glide ratio.

A sailplane has a best glide ratio of 23:1. How many feet will the glider lose in 8 nautical miles?
- (a) 1,840 feet
- (b) 2,100 feet
- (c) 2,750 feet
(Source: 2024 Private Pilot Test Prep; ASA Test Prep Board)
This question might look simple, however, it’s easy to trip over small things when trying to work out how the answer one calculates is supposed to match one of the possible answers provided in the question. It helps to dig in, calculate things with the best numbers we have, and then take a step back and realise that the conversion factors implicit in the three answer options are only approximate. In other words, we’ll have to put any potential physicist pedantry to one side in this case.
There are a few things to note first before we dig in here:
- A large component of the question is just converting between quantities of different units.
- There is some implicit knowledge required here, which is unfortunately not mentioned as part of the question. In particular, it’s necessary to know beforehand the number of feet in one nautical mile.
- The numbers given as possible answers are only approximate; they will not correspond to exact distances in feet. That this is the case is only clear when one knows how many feet there are in one nautical mile (to be mentioned later).
- The words “sailplane” and “glider” can be used interchangeably and refer to the same thing.
With that out of the way, let’s analyse the question.
The glide ratio tells us how many units of distance a glider can fly forwards for every unit of altitude that it loses. In the case we have here, the glide ratio is 23:1 meaning that, if we use the units of metres, the glider will fly 23 metres forwards for every metre of altitude that it loses. Another way of looking at it: if your glider is 1 m above the ground, then you will be able to fly 23 m before hitting the ground. This calculation also works for other units (as is the case in this example). Thus, for every foot of altitude we lose, we can fly forwards 23 feet or, equivalently, for every 23 nautical miles we travel forwards, we will lose 1 nautical mile of altitude. Note that the units for the forward distance and the altitude loss have to be the same for this to give a ratio, which is a unitless quantity.
We can also understand this situation graphically via the drawing below, where \(\Delta l\) is the distance the aircraft travels forward and \(\Delta h\) is the altitude the aircraft loses over that horizontal distance.
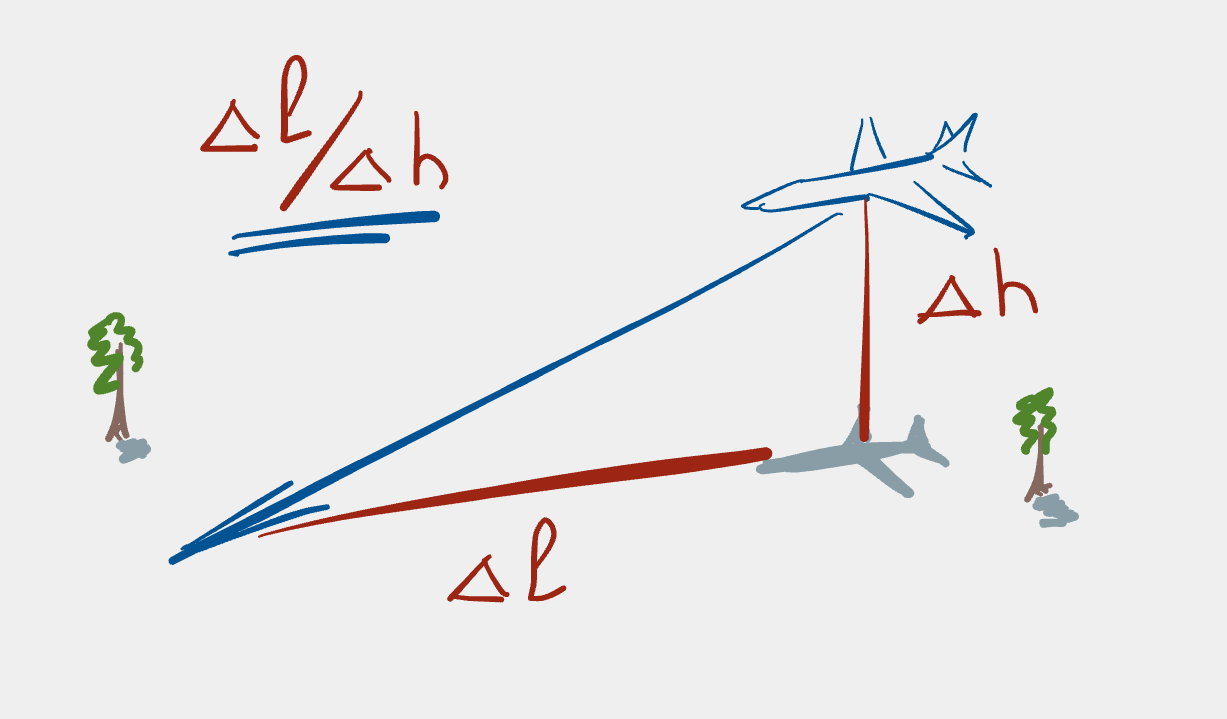 (Source: Glide ratio, lift-to-drag and their (in)dependence on aircraft weight, Alexey Gronskiy)
(Source: Glide ratio, lift-to-drag and their (in)dependence on aircraft weight, Alexey Gronskiy)
One difficulty with the question is that we’re given a distance in nautical miles but have to calculate an altitude loss in feet. Therefore, we could choose to convert the 8 nautical miles horizontal distance into feet at the beginning, or we keep using nautical miles the whole way through the calculation and convert them to feet at the end or we could just do everything algebraically and only enter numbers (and do any unit conversions) at the end; let’s do it that way now.
The algebraic path
Taking the algebraic path (which is a bit more general and doesn’t require us to juggle big numbers the whole time) is probably the more physicist-like approach. I mean, why do heaps of hard work when we can just move symbols around to get the answer, right?
We have the relationship that the glide ratio is 23:1 (i.e. 23/1). We know that the glide ratio is equal to the distance travelled divided by the altitude lost, hence we have this relation:
\[\frac{\Delta l}{\Delta h} = \frac{23}{1}\]Note that the glide ratio is unitless, which means that \(\Delta l\) and \(\Delta h\) have to be in the same units, i.e. if \(\Delta l\) is in nautical miles, then (and it doesn’t matter how silly the numerical value looks) \(\Delta h\) must also be in nautical miles.
We’ve been given \(\Delta l\) in the question (8 nautical miles) and therefore have to solve this equation for \(\Delta h\), the altitude loss. Solving the above equation for \(\Delta h\) goes like this:
\[\begin{eqnarray} \frac{\Delta l}{\Delta h} &=& \frac{23}{1} && \text{(multiply by $\Delta h$)}\\ \Rightarrow \Delta l &=& 23 \cdot \Delta h && \text{(divide by 23)}\\ \Rightarrow \frac{\Delta l}{23} &=& \Delta h && \text{(rearrange to put $\Delta h$ on the left-hand side)}\\ \Rightarrow \Delta h &=& \frac{\Delta l}{23} \end{eqnarray}\]We can now calculate what \(\Delta h\) must be numerically. Using \(\Delta l =\) 8 nautical miles, we have:
\[\Delta h = 23/8 = 0.3478 \text{ nautical miles (to 4 decimal places)}\]Ok, so how far is this in feet? By looking up the Wikipedia page for the nautical mile, we have the relationship:
\[1 \text{ nautical mile} \approx 6,076 \text{ feet}\]Note that this value is only approximate because there are probably a few inches involved in the unit conversion that aren’t being specified here.
We now just need to convert \(\Delta h\) from nautical miles into feet. We do this by multiplying the value we got for \(\Delta h\) by the conversion factor from nautical miles to feet, in other words:
\[\begin{eqnarray} \Delta h &=& 0.3478 \text{ nautical miles}\\ &=& 6076 \cdot 0.3478 \text{ feet}\\ &=& 2113.3913 \text{ feet} \end{eqnarray}\]This value doesn’t equal any of the given options in the question, nevertheless, it’s closest to answer (b), therefore we conclude that the answer is (b) 2,100 feet.
Why can we make this conclusion confidently? Well, the conversion from nautical miles to feet isn’t a “round” number (i.e. a number ending in something like a ‘0’); also the relationship between 23 (from the glide ratio) to 8 (the horizontal distance travelled in nautical miles) means that they don’t divide into each other cleanly either. Therefore, none of the values here is going to give the kinds of “clean” “nice” “round” numbers such as those provided as possible answers to the question. Thus we can conclude that it’s more important for the provided answer to be within 1–2 significant digits of what one calculates exactly rather than providing an exact value in the question.
Jumping straight in, feet, erm, boots and all
So how is the accepted answer explained in the textbook? The short answer to that question is that one calculates the glide distance in feet for one nautical mile and then scales that distance up by the number of nautical miles given in the question. Let’s take a closer look at this way of approaching the situation.
As discussed in the previous section, the glide ratio is the ratio of forward to downward motion (i.e. how many units of distance we travel horizontally in proportion to one unit of height loss). In this case, we have a glide ratio of 23:1, which we can write as a fraction like so:
\[\frac{23}{1}\]If we travel one nautical mile forwards, we will have lost some proportion of a nautical mile in height. This is an (as yet) unknown quantity that we wish to work out. As is common with unknown quantities, let’s call it \(x\).
Let’s also consider how many feet there are in one nautical mile (NM): this is approximately 6,000 feet/NM and is the conversion factor used in the textbook. This, if we move horizontally for one nautical mile, then we’ve flown 6,000 feet forwards. We know from the glide ratio that this number is 23 times greater than the height lost (in feet/NM) which is our unknown quantity \(x\). Thus, 6,000 feet/NM divided by \(x\) will be equal to the glide ratio. Writing this in more mathematical terms, we have:
\[\frac{23}{1} = \frac{6000 \text{ feet/NM}}{x \text{ feet/NM}}\]Remember that this is a ratio and hence a unitless quantity, which is why it’s important to use the same units (feet/NM) in the division on the right-hand side of the above equation.
If we multiply both sides of this equation by \(x\) we get:
\[\frac{23}{1} \cdot x = 6000\]now dividing by 23, we get an expression for \(x\) on its own:
\[x = \frac{6000}{23} = 261 \text{ feet/NM}\]where we round up the value to the nearest foot.
Therefore, we lose 261 vertical feet (i.e. the downward motion is 261 feet) for every 6,000 feet (i.e. nautical mile) of forward distance.
How many feet of downward motion do we have, then, for 8 nautical miles? To calculate this, we just multiply our value for \(x\) by 8. This value is called the total sink in the textbook.
\[\text{total sink} = 8 \text{ NM} \cdot 261 \text{ feet/NM} \approx 2100 \text{ feet}\]Where, again, we make an approximation to obtain the final value, thus confirming our result from the previous section and reaffirming the accepted answer, (b) 2,100 feet.
Original post
This was originally posted as part of the after-school-help project.
Support
If you liked this post and want to see more like this, please buy me a coffee!